The problem statement says that the heating element is on for a long time, so we can assume that the temperature of the water is constant. This means that the water loses
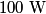 to the environment. When the heating element is removed, the rate that energy is lost will be approximately the same at least during the amount of time it takes the water to cool by to the environment. When the heating element is removed, the rate that energy is lost will be approximately the same at least during the amount of time it takes the water to cool by 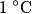 . The density of water is approximately . The density of water is approximately 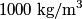 and one liter is and one liter is 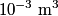 . Therefore, the mass of water in the pan is . Therefore, the mass of water in the pan is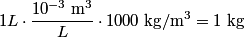 So, the answer is 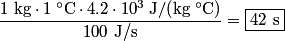 Therefore, answer (B) is correct. |